Calculating Rotoscope Angular Error Potential

Using 3D model rotoscoping allows calculation of potential error caused by estimated camera positioning.

As an example, the position used in the previous sample rotoscope will be checked.

Here is a deliberately rough estimation for the camera position:

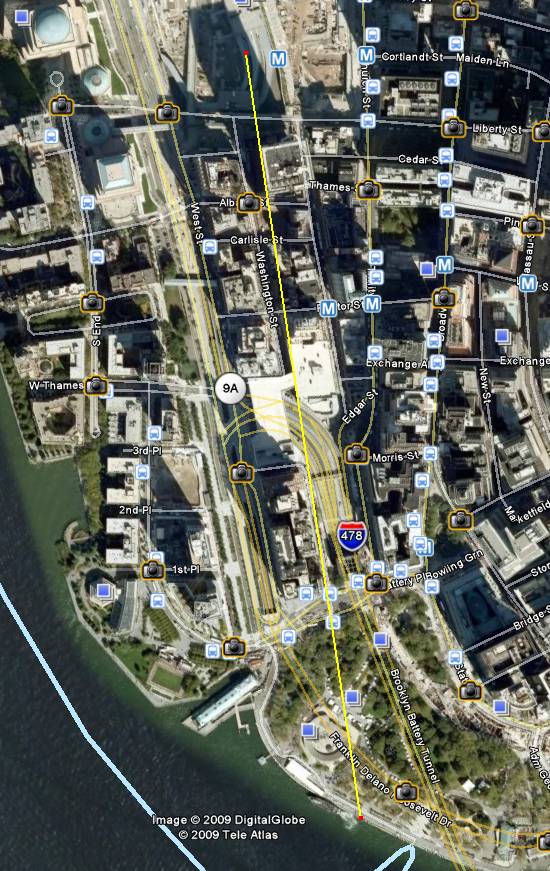
Potential placement error can of course exist for the position of both points, however, the accuracy of the target point (the top point) can be determined to high precision, and so initial error calculation will focus upon the camera location. Target accuracy will be detailed later of course.

If we assume a significant 100ft camera placement error, which is also assumed to be in a direction perpendicular to the ‘line of sight’ to make the calcs simple, then we can very easily calculate the change in lateral angle.

The distance between the two points is: 3342ft

Angle = atan(100/3342) = +/- 1.7139 degrees.

100ft closer to the tower (impossible as the cameraman was on a ferry) would increase that angle error potential to atan(100/3242) = +/- 1.7667 degrees.

100ft further from the tower (unlikely as the ferry was apparently docked) would decrease that angle error potential to atan(100/3442) = +/- 1.6641 degrees.

100ft in all directions from the selected spot looks like this:

What is gained from this Calculation ?

Video rotoscoping is used to verify the impact orientation. This calculation allows us to determine the accuracy of the viewing angle. The viewing angle accuracy in turn directly defines the accuracy of the rotation of the tower model, and the 3D aircraft model.

It has been previously shown that in order for the aircraft model to match video footage, it must be rotated 9.5 degrees from the angle used by NIST.

If our draft camera location is within 100ft of the actual camera location, the rendered view, specifically the rotation of the tower and aircraft, is therefore within around 1.7 degrees of the actual value.

How far off would the camera location have to be to generate a 9.5 degree error ?

Perpendicular distance = 3342 * tan(9.5 degrees) = 559.1166ft.

In reality we can place the camera with an accuracy well within 100ft, as not only have the occupants of the ferry upon which the footage was taken stated their specific positions, but there is also additional photographic footage available from the same time aboard the same ferry, from a very slightly different viewing position, taken by a different person. This allows additional clarification to be performed.

Beyond multiple footages, from essentially the same location, is the fact that other buildings within the viewing frame allow for parallax-based positioning to be performed, significantly increasing camera viewpoint accuracy.

The Effect of Parallax

As other buildings in the frame are closer to the camera, accurate lateral camera positioning can be determined by taking account of the relative ‘overlap’ between near-field (foreground) and far-field (background) building features. In this case the Downtown Athletic Club and surrounding buildings in the foreground, and WTC 1 and 2 in the background.

Ten Foot (10ft) Lateral Change in the Camera Position:

Hundred Foot (100ft) Lateral Change in the Camera Position

As can be seen, the background features (WTC 1, 2 and the two sample aircraft (NIST and TEST)) show very little change from the 10ft camera shift, and relatively minor change from the 100ft shift.

However, the relative position change and overlap of the foreground buildings is VERY significant, and very noticeable.

By ensuring accurate positioning and scaling of the included buildings, cross-referencing between the two sources of visual footage in the same rough location (the same ferry) to determine good quality camera placement, and all of the discussed factors it will clearly be possible to specify camera position well within the 100ft margin discussed previously. A positional error within 10ft (0.17 degrees) is entirely practical.

Progress Summary

It has been shown that to match video footage from a sample camera location (within that 100ft boundary) with a maximum horizontal/lateral angular error of roughly 1.7 degrees, requires the aircraft to be rotated by 9.5 degrees along the horizontal axis (and 3 vertically).

Even at this point, prior to finalising the specific camera and additional building positioning, an error in the NIST value of at least 7.5 degrees has been identified.

If a camera placement is determined within a 100ft error of margin, the NIST angle is out by over 7 degrees.

If a camera placement is determined within a 10ft error of margin, the NIST angle is out by over 9 degrees.

Any way you look at it, such a significant error has huge implications for all of the subsequent NIST WTC 2 impact damage estimations, and therefore similar implications for the subsequent collapse initiation studies which are fundamentally based upon the impact damage assessments.

Still draft details for discussion at the911forum only.

Part 3 will include details such as determination of slew (differences in trajectory and orientation), additional building placement and camera location

Regards,

Femr2